Prize Competition
From Order to Chaos: The Prize Competition in Honour of King Oscar II
by Mikael Rågstedt
Former Librarian at Institut Mittag-Leffler
Please verify and be careful about any phishing and scam attempts from external companies.
All conferences and research programs at IML are free of charge.
We will not ask you for any payments regarding your accommodation or travel arrangements
From Order to Chaos: The Prize Competition in Honour of King Oscar II
by Mikael Rågstedt
Former Librarian at Institut Mittag-Leffler

The main purpose of this page is to present digitizations of three documents by Henri Poincaré from the early history of the prize competition in honour of King Oscar II and arranged by Gösta Mittag-Leffler. The unique originals are preserved at Institut Mittag-Leffler in Djursholm, Sweden. To explain the significance of these manuscripts a summary is given below of how the dramatic story unfolded, followed by links to the documents and a list of some references for further reading.
In 1885 Gösta Mittag-Leffler could look back at a successful start on his career as the first professor in mathematics of the newly founded Stockholms högskola (later to become Stockholm University). After his education and doctor’s degree from Uppsala, he had spent three years in Paris and Berlin while he forged firm bonds with many leading European mathematicians.

He then turned to Helsinki where he broadened his horizons as a dedicated and strong-willed professor. Four years later, in 1880, he returned to his native Stockholm. The new principles on which Stockholms högskola was founded gave Mittag-Leffler the opportunity to work out his ideas of how mathematical education and research should be organized and promoted. He attracted several talented postgraduates, and managed to engage Sofia Kovalevskaya as lecturer and later full professor at the department. The journal Acta Mathematica which he founded in 1882 was right from the beginning received as a leading international publication. It established itself as an effective transmitter of new mathematical ideas between France and Germany in the aftermath of the Franco-Prussian War (1870-71).

One of Mittag-Leffler’s inventive ideas in promoting Acta Mathematica was to turn to King Oscar II of Sweden and Norway, both for financial support of the project and as the first enlisted subscriber. In 1884 another grand idea from Mittag-Leffler had matured. Again involving King Oscar, he now wanted to arrange an international prize competition in mathematics honouring the 60th birthday of the king. It seems that Mittag-Leffler first revealed his plan to Kovalevskaya. We find a short reference in a letter to her from 4 May 1884. A month later itis clear from another letter by Mittag-Leffler that she had by then discussed the prize with Karl Weierstrass. In July Mittag-Leffler for the first time briefed Weierstrass on the plans.

It was first decided to form a small prize jury consisting only of three members: Mittag-Leffler himself, acting as administrative and coordinative liaison with his mentors and friends Karl Weierstrass in Berlin and Charles Hermite in Paris. They were not only the two dominant mathematicians of the older generation, but there was also a special sympathy between them. This would be a prize awarded not for past contributions, but for a solution to an unsolved problem specified by the committee. In order to attract the best mathematicians from different branches of mathematical analysis they agreed on four questions. The first three seem to have been proposed by Weierstrass and the fourth by Hermite. It took a year of intense discussions to settle all the details, which were then officially announced in Volume 7 of Acta Mathematica in the middle of 1885.

The special features of this competition was the international and ambitious appeal, and the connection not to an academy or institution, but to the journal Acta Mathematica, where the winning entry finally was to be published. The prize consisted of a gold medal and 2,500 Swedish kronor. (As a comparison, Mittag-Leffler’s annual salary as professor was 7,000 kronor.) The memoirs should be submitted before 1 June 1888 (almost three years after the announcement), with anonymity maintained through a motto on an enclosed sealed envelope containing the name of the author.
The first question was a formulation of the classical n-body problem in celestial mechanics, and it attracted the most attention:
Weierstrass nourished great hopes that there would be a method of solution based on a simple fundamental idea, and that such a solution could help conclude whether the system was stable. In applying this formulation of the n-body problem as a model of the solar system, could it be excluded that the planetary orbits might alter radically over a long time, or even that one planet be thrown out of the system?

Henri Poincaré (1854-1912) had been in the focus right from the start. He was the most brilliant mathematician of the rising generation and had already established a special connection with Mittag-Leffler and Acta Mathematica, where his first important series of articles appeared in the earliest volumes. The committee knew very well that Poincaré had the capacity to attack any of the four questions. In correspondence with Mittag-Leffler he made clear his intention to grapple with Question 1. In May 1888, after hard work and many doubts, he submitted his memoir Sur le problème des trois corps et les équations de la dynamique. As for the anonymity, well …, accompanying the memoir were two letter notes, one to the prize jury and one to Mittag-Leffler.

A list of all the twelve manuscripts received by June 1888 was published in Volume 11 of Acta with their identifying epigraphs. It turned out that five of the authors had attempted the prestigious Question 1, one had tried Question 3, while six treated a subject of their own, which remained a secondary option. Only four of the authors have been identified: in addition to Poincaré also Paul Appell, Guy de Longchamps and Jean Escary.

In the spring and summer of 1888, Mittag-Leffler was travelling in Europe. He stayed in close mail contact with his assistant and gifted former student Edvard Phragmén, who became an active editor in Stockholm. Handwritten copies of Poincaré’s memoir were procured for Weierstrass and Hermite.
Although no entry had actually solved any of the questions, Mittag-Leffler and his jury were soon of the preliminary opinion that Poincaré was in a class of his own, that Appell should be awarded a second honorary prize, and that no other entries needed much further examination.
Poincaré had decided to attack the problem in a new way. He elaborated on several ideas and results from his earlier works on differential equations. Instead of only trying to follow the motion of every mass point at all times in terms of infinite trigonometric series, as had been the traditional approach for a long time, he focused his attention on qualitative aspects of the entire system’s state of motion in phase space. Here he studied the flows by innovative geometrical as well as topological methods that impressed Weierstrass. This included following the behaviour of orbits in the immediate neighbourhood of periodic orbits, and to study their iterated appearance on a cross section transverse to the flow in phase space (this is Poincaré’s stroboscopic first return map). We also find the first presentation of Poincaré’s well-known recurrence theorem.
He started with new ideas about periodic solutions, introducing certain associated constants, so-called characteristic exponents, whose properties could give information about the stability, and he found and described a new type of solutions which asymptotically approached an unstable periodic solution when moving forwards or backwards in time. He labelled them asymptotic solutions.
To obtain tangible results for the memoir he concentrated much of his efforts on the three-body problem, and even on the restricted, planar and circular case in which two primary bodies of finite mass are not influenced by the third body of negligible mass. The problem is then reduced to two degrees of freedom; that is, four coordinates are needed to describe the system, which may be reduced to three because there is a conserved quantity. In this case the asymptotic solutions formed two asymptotic surfaces. Finally after almost 300 handwritten pages (including the appendices) his new concept of integral invariants and the subsequent geometrical arguments led to a claim of stability for this system.
Original epigraph

Printed epigraph

- "The whole edition was destroyed"
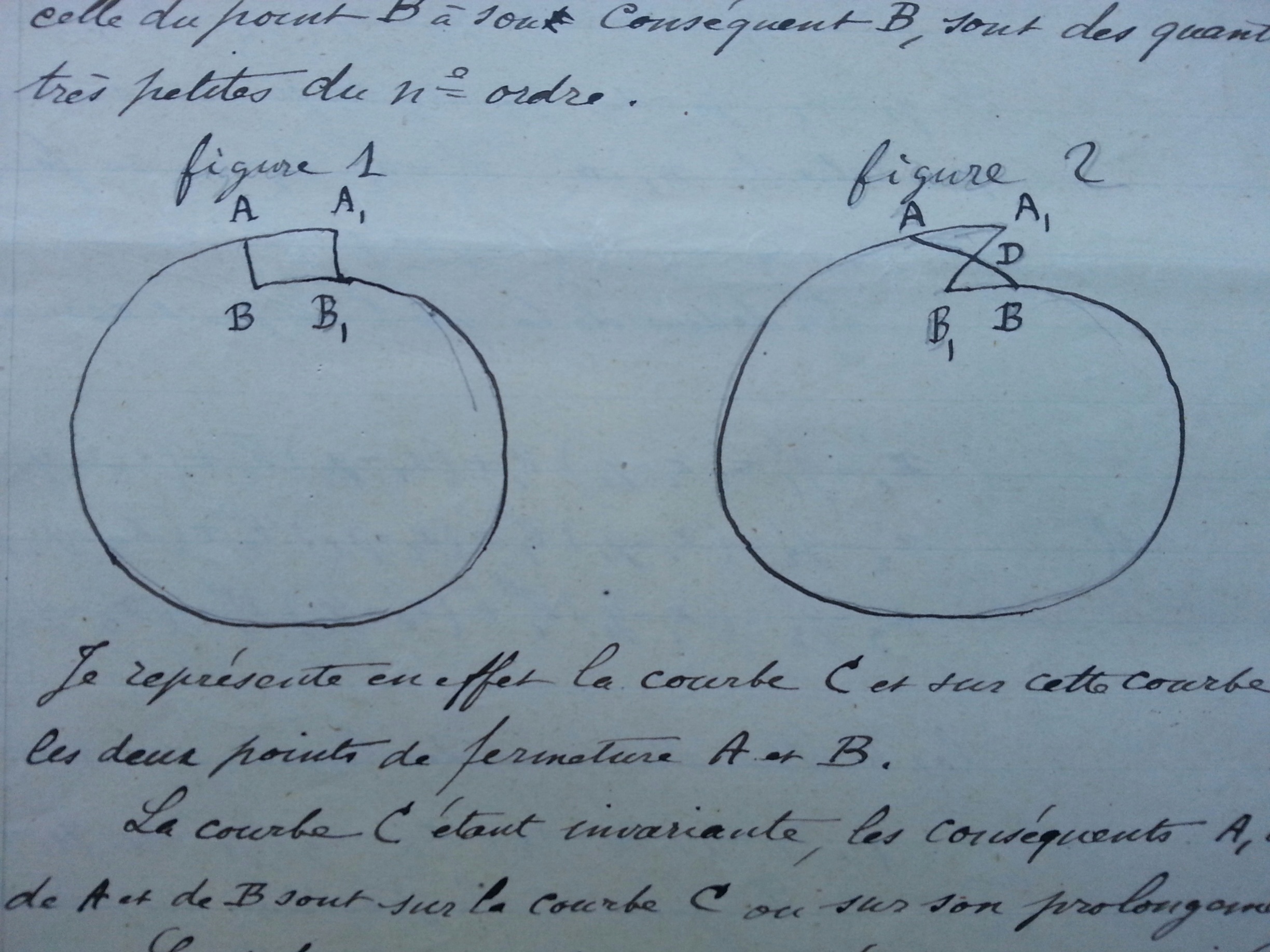
Poincaré's original handwritten figures 1 and 2
Poincaré's original handwritten figure 3

Poincaré's original handwritten figure 7
Poincaré's original handwritten figure 9
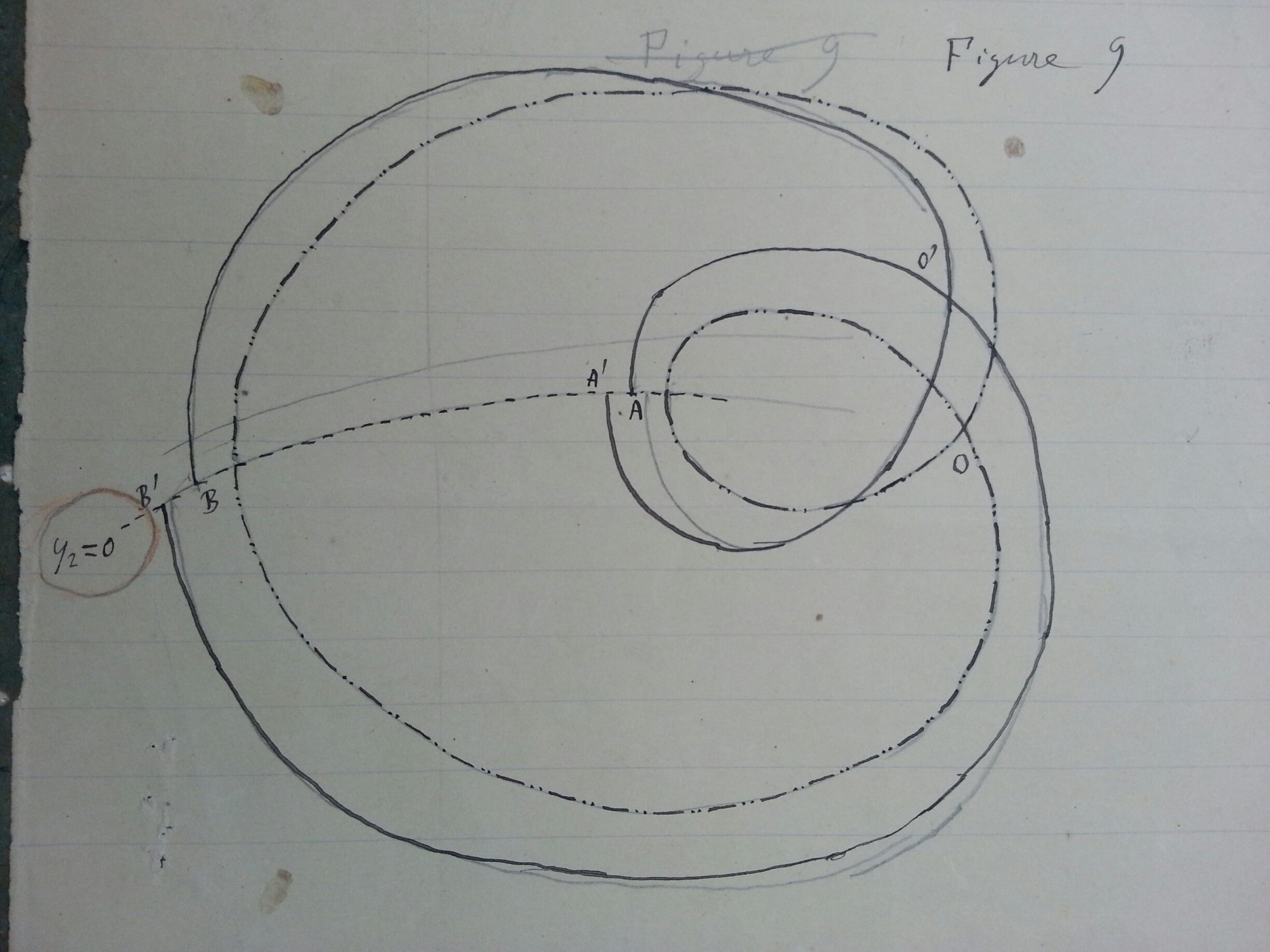
So far so good, it seemed. The members of the committee had difficulties, however, in understanding Poincaré’s long work, written in his typical, rather intuitive style with omission of many details. Mittag-Leffler’s plan was to meet Weierstrass in August during a vacation in Wernigerode on the north slopes of the Harz mountains to settle final matters. Now it turned out that other mathematicians as well were drawn to the small company at the picturesque resort, and all with their own agenda. Instead of a peaceful working session, the summer weeks became full of drama and conflicts. Anyhow, the jury finally agreed that the winning memoir needed additional clarifications from Poincaré (against which ethical objections were raised, apart from the anonymity!). Poincaré complied by sending a series of appendices (notes) over the next few months, growing to around 100 added pages. In mid November Weierstrass sent a short report to Mittag-Leffler and concluded, “You may tell your Sovereign that this work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics.” It was clear that Poincaré’s new concepts, techniques and results were path-breaking not only in the theory of dynamical systems, but in other mathematical fields as well.
Due to the poor and unstable health of Weierstrass, his full report on Poincaré’s winning memoir had to be postponed. So when Mittag-Leffler made his final presentation to the king on 20 January 1889, the day before the monarch’s 60th birthday, only the brief summary from Weierstrass was enclosed in the general report. For the winning entry Henri Poincaré received the sum of 2,500 kronor together with a gold medal. Paul Appell was also rewarded with a gold medal in addition to the honourable mention. For various reasons the prize ceremony didn’t take place on the king’s birthday, but the announcement was made public that day. Instead Poincaré received his prize from the hands of the Swedish ambassador in Paris later in March. Mittag-Leffler also informed the French Academy of Sciences of the news. (See Comptes Rendus, 108:8, 1889.)
While awaiting additional clarifications from Poincaré, the printing of the memoir was put on hold. In the meantime the respected Finland-Swedish astronomer Hugo Gyldén launched an attack on his colleague Mittag-Leffler during a meeting at the Royal Swedish Academy of Sciences. Gyldén claimed that he had already published the main results in Poincaré’s memoir. After discussing the matter with Poincaré, Mittag-Leffler retorted by explaining that notions like “proof” and “convergence of infinite series” mean different things to astronomers and mathematicians. Poincaré at that time appreciated Gyldén’s work for its practical implications. Still, the Swedish astronomers sided with Gyldén in the conflict (without understanding the details, of course).
Finally, in July 1889, Mittag-Leffler decided that it was time to take action and print Poincaré’s dissertation, with all its added appendices. This went on until mid November, when the next volume of Acta was due to appear. Phragmén went on with the editorial work, and from the summer he was the only one who still raised objections to conclusions in the memoir that he didn’t understand, first to Mittag-Leffler and Weierstrass, and then directly in contact with Poincaré. The queries forced Poincaré more and more to confront his arguments in detail.
On the last day of November 1889, an ominous telegram reached Mittag-Leffler. Poincaré briefly told him to stop the presses. He had found an error. An explanation was expected by letter the next day. After a sleepless night Mittag-Leffler could then read that the error was graver than Poincaré had first thought. “It is not true that the asymptotic surfaces are closed”, he wrote.
In his restricted three-body problem Poincaré had described two asymptotic surfaces associated with an unstable periodic solution: a stable manifold (the inset) consisting of all neighbouring solutions attracted to the periodic solution, and an unstable manifold (the outset) formed by the corresponding solutions repelled from the periodic one. Poincaré had automatically assumed that the two asymptotic surfaces glued together smoothly to form a single closed surface sheet, and in particular that no intersections occurred. This would imply the existence of another integral invariant, and the claimed stability of the system. Geometrically it means that each solution curve is confined to a limited region of phase space and cannot pass through the boundary of the closed invariant asymptotic surface. Instead Poincaré had now found that the two asymptotic surfaces could intersect transversely and, as it seemed, in a very intricate manner.
Poincaré was clearly confused and distressed at his new discovery and its consequences. It was too early for him to give an estimate of how much could be saved of the results. He asked Mittag-Leffler whether he still deserved the prize.
Images of several damaged careers must have passed through Mittag-Leffler’s mind: apart from his own, also those of Poincaré, Weierstrass and Hermite, not to mention the disgrace brought on the celebrating King Oscar. His adversaries would revel in his misery. It was especially aggravating that a substantial number of prepublished copies of Poincaré’s memoir had already been distributed around the world. But Mittag-Leffler acted swiftly as usual and spared no effort in trying to remedy the daunting situation he faced:
After intense work in December, and over Christmas and New Year, Poincaré was ready to submit a substantially revised memoir on 5 January 1890. He had altered some of the implicit assumptions which had turned out to be precipitate. Instead of stability for the restricted three-body problem, he had come to the inevitable conclusion that chaotic motion could occur, as we would now call the phenomenon. Furthermore, the appendices, Notes A-I, had been incorporated into the text. The manuscript is now kept at Institut Mittag-Leffler, and consists of old printed pages amended with handwritten corrections and additions, mixed with new handwritten sheets.

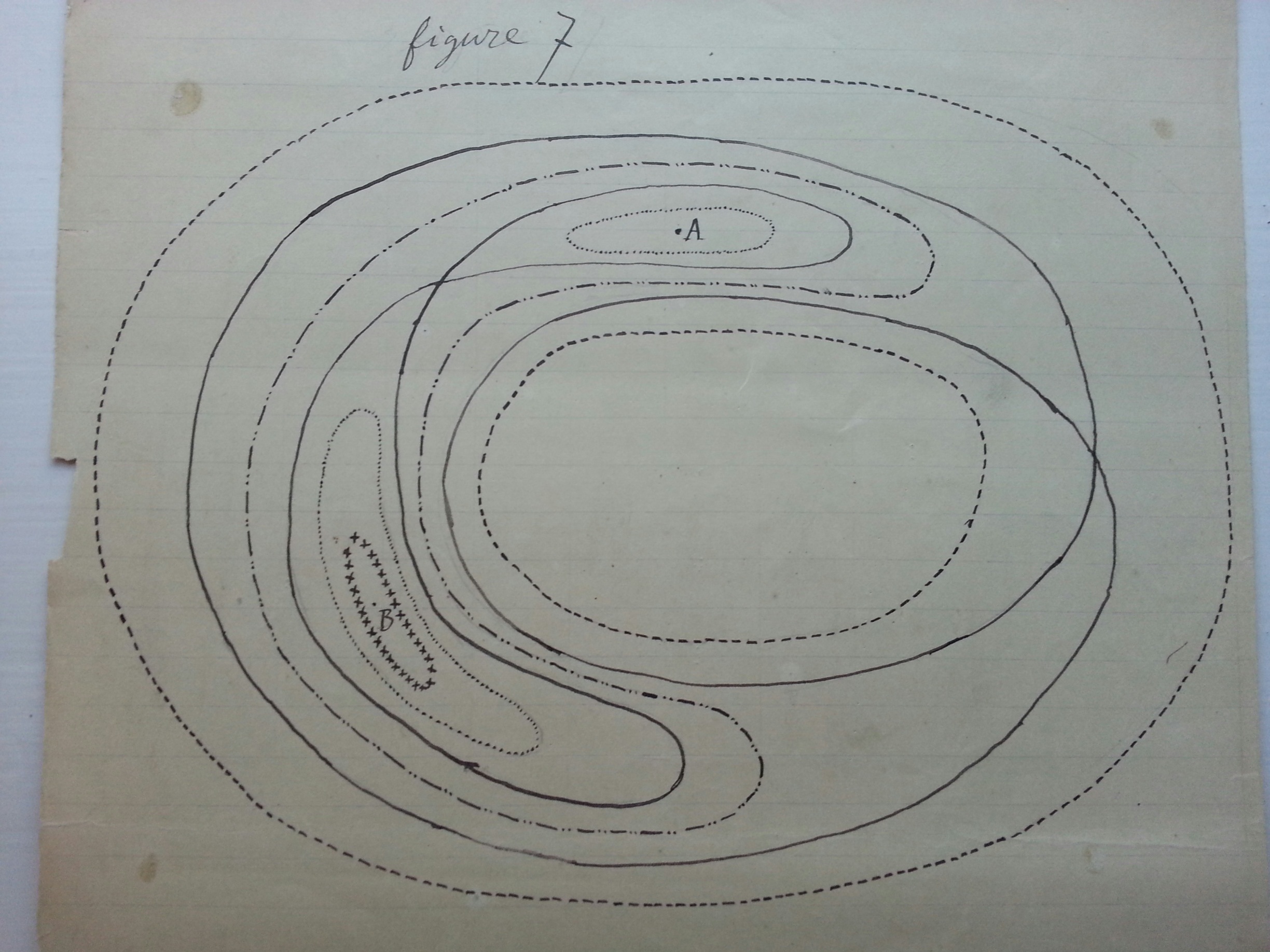
By studying the asymptotic surfaces projected on his transversal cross section under the first return map, thereby reducing them to invariant asymptotic curves, he managed to get a glimpse of the new complexity. When he had to accept that the inset and outset curves in fact could intersect each other (unlike in the case of actual solution curves in phase space!), he found to his astonishment that they then had to intersect at an infinity of points. By iteration the original intersection point generated one sequence of new intersections on the cross section when the outset trajectory in phase space was extended forward in time, and another similar sequence of points when the inset trajectory was extended backward in time and hit the cross section. Both sequences approached the same fixed point on the cross section (corresponding to the periodic solution in phase space). He later called the intersections homoclinic points. These doubly asymptotic points on the cross section correspond to Poincaré’s famous homoclinic trajectories or doubly asymptotic solutions in phase space: they asymptotically both leave and return to the same unstable periodic solution. As if this was not enough Poincaré saw further implications. Due to the stretching and folding of the outset (forward in time) and of the inset (backward in time) close to the fixed point (characteristic of chaotic motion), an infinity of new inset-outset intersections appears between the original ones, all coming from distinct homoclinic trajectories in phase space. The iterates of each such homoclinic point give rise to a new infinity of homoclinic points in the same way. Poincaré noted that all these intersections together, even though countably infinite, create an intricate mesh of infinitely fine web, a homoclinic tangle. He never attempted to make a schematic drawing of it.

The full picture in three dimensions really stretches our visual imagination: the two asymptotic surfaces now intersect in infinitely many intertwined homoclinic curves (trajectories). In a finite region of phase space, an infinite number of tiny stretched-and-folded volumes enclosed by small pieces of the inset and the outset surfaces separate different kinds of orbits. Instead of a simple inside and outside of the closed asymptotic surface as in the solvable, stable two-body problem, we have here a situation where the sensitive dependence on initial conditions renders it meaningless to make predictions of the fate of an orbit. And Poincaré’s model of the restricted three-body problem was the simplest extension into the unknown that he could find!
The printing resumed in late April 1890, but Poincaré’s final memoir of 290 pages only appeared in December 1890, in Volume 13 of Acta, together with Appell’s contribution and Hermite’s report. Weierstrass’s full report on the Poincaré memoir was never completed.
The Swedish sovereign, in whose honour the prize had been established, was probably in blissful ignorance of all the twists and turns between the contemporary princes of mathematics.
Is it possible to point out a specific “error” or “mistake” in Poincaré’s original version? The Corollary to Theorem III, which claimed that an invariant curve under certain conditions had to be closed, formed the basis of his later stability results. In the final memoir a new Theorem III replaced both the earlier Corollary and Theorem. In the proof, he now inspected four possible forms of the curve, three of which could be excluded, so that the only remaining case was for the curve to intersect itself. He had failed to see this alternative in the first version. There he had also made drawings for two of the cases, and he retained them in the revised memoir. But he probably never had time to add a picture of the correct self-intersecting curve (for a drawing see Barrow-Green [1997, Figure 5.5.iii].
Edward Phragmén’s persistent questions didn’t focus on these geometrical results, but rather on the corresponding analytical side where Poincaré looked for an understanding in traditional terms of certain infinite series defining the asymptotic solutions and surfaces. The series were expanded in powers of the small but finite mass of one of the two primary bodies. In the first version he had tacitly generalized an argument of convergence for these series to all types of Hamiltonian systems. In a letter to Poincaré from July 1889 Mittag-Leffler forwarded some questions posed by Phragmén about the series and how we could know that they really converge. Poincaré attempted to give an explanation by sending his last two appendices (Notes H-I). Phragmén, still not satisfied, sent two more letters directly to Poincaré in the autumn, according to Mittag-Leffler’s recollections 20 years later (lecture drafts in Swedish at Institut Mittag-Leffler).
In the revised version Poincaré had come to the conclusion that the infinite series did not converge in the case of the restricted three-body problem (and of autonomous Hamiltonian systems in general). Instead such series were of a type that he had studied earlier and called asymptotic series: not convergent but still of great value in approximations. Here was a link to the world of the astronomers. Phragmén’s role was clearly but briefly acknowledged in the revised introduction. But put under pressure by Mittag-Leffler, Poincaré gave no hint to the readers as to the nature of the error.
A small irony in this story is that the original epigraph Nunquam praescriptos transibunt sidera fines, used to identify Poincaré as the author, was still seen in the revised memoir, despite the clear reference to stability: Never will the heavenly constellations cross their prescribed bounds!
Since Poincaré himself found it difficult to grasp the startling consequences of his discovery of homoclinic points, it comes to no surprise that very few mathematicians and astronomers at the time could understand his results. Poincaré produced no more epoch-making results of this kind in celestial mechanics during his lifetime, but between 1892 and 1899 he composed the important comprehensive three-volume treatise Les méthodes nouvelles de la mécanique céleste, where his discoveries were elaborated in more detail.
A remarkable epilogue to King Oscar’s prize competition occurred when the Finnish mathematician and astronomer Karl Sundman actually found a complete solution to Question 1 in the general case of three bodies. In articles between 1907 and 1912 he gave a proof of the convergence of an infinite series solution to the three-body problem for almost all initial values, using well-known results. Although the methods used are relatively simple, the very slow convegence renders the series solutions unusable for practical purposes, and they provide no qualitative insight into the motion of the bodies. Even though Sundman’s achievement was praised and received attention in the decade to follow, it soon faded into oblivion. In 1991 Qiudong Wang managed to generalize Sundman’s solution to the general n-body case. For references, see Sundman [1912] and Wang [1991].
The astronomers now instead turned their interest towards new discoveries outside our solar system and galaxy, at the expense of celestial mechanics. They found the theoretical side too mathematical, while further practical progress had to wait for (digital!) computers to enter the scene. Among the mathematicians a few great names continued Poincaré’s qualitative approach to dynamical systems, especially George Birkhoff, but also to some extent Aleksandr Lyapunov and Jacques Hadamard. Puzzling chaotic behaviour made its appearance now and then in physicists’ experiments and models until 1963, when an article by Edward Lorenz soon advanced modern chaos theory to all corners of science and gradually even became a commonplace in the media.
But we should never forget the man who first caught a glimpse of chaos, and the story of how he finally a November evening in Paris 1889 drew the tangled consequences of the homoclinic points he had found when correcting his memoir.
The three central documents by Henri Poincaré in this story were digitized at the Center for History of Science, one of the research institutions of the Royal Swedish Academy of Sciences. Originally in very high resolution (pdf files of ca 600-800 MB), they have been reduced here to smaller pdf files, some split in to parts, more convenient to download and manage, and sufficient for most purposes. Included below is also the final published memoir.
The documents may be downloaded and shared for personal use, links are found at the bottom of this page.
(1) Poincaré’s original manuscript (May 1888). Until 2011 we thought that this manuscript was lost, but by a lucky coincidence it turned up again. Thanks to a generous donation by the former owner, Ulf R. Johansson, it is now back in the Mittag-Leffler archives. We believe that this handwritten manuscript is the actual version that Henri Poincaré submitted as his contribution to the competition in May 1888. The pen was probably held by his wife Louise, who often served as his private secretary. But Henri’s handwriting can sometimes be recognized in modifications, margin notes, footnotes and the epigraph. Also the figures are certainly drawn by him. The added appendices (notes) must have been incorporated later. Notes A-G are complete except for the missing last page (12 lines) of Note G. The last two, Notes H-I, are absent. This makes sense, since they didn’t come from Poincaré until after the first printing had started. Editorial markings in pencil indicate that this manuscript was sent to the printers. The first title page bears the handwriting of Edvard Phragmén, the editorial assistant. The text of the manuscript seems to agree closely with that of the first printed version.
(2) The first printed version (November 1889). To our knowledge there are only two copies left today, both at Institut Mittag-Leffler. They were bound by Mittag-Leffler, and the one digitized here carries the handwritten note (in Swedish) “The whole edition was destroyed. M.L.”
(3) Poincaré’s revised manuscript (January 1890), which consists partly of new handwritten pages, and partly of handwritten corrections and modifications to the first printed version. The revised manuscript forms the basis of the printed official version. The order follows the handwritten page numbers in blue colour. Pages 88-89 seem to be missing. The document came to Institut Mittag-Leffler on 22 May 1978 from Phragmén’s collected papers.
(4) The final memoir published in Acta Mathematica, Vol. 13, 1890. This is a scanning in lower resolution.
Andersson, K. G., Poincaré’s discovery of homoclinic points. Arch. Hist. Exact. Sci., 48 (1994), 133-147.
Barrow-Green, J., Oscar II’s prize competition and the error in Poincaré’s memoir on the three body problem. Arch. Hist. Exact. Sci., 48 (1994), 107-131.
Barrow-Green, J., Poincaré and the Three Body Problem. Amer. Math. Soc., Providence, RI, 1997.
Barrow-Green, J., Henri Poincaré, memoir on the three-body problem (1890), in Landmark Writings in Western Mathematics, 1640-1940, pp. 627-638. Elsevier, Amsterdam, 2005.
Barrow-Green, J., The dramatic episode of Sundman. Hist. Math., 37 (2010), 164-203.
Chenciner, A., Poincaré and the three-body problem, in Henri Poincaré, 1912-2012, pp. 51-149. Poincaré Seminar 2012. Birkhäuser, Basel, 2015.
Diacu, F., The solution of the n-body problem. Math. Intelligencer, 18:3 (1996), 66-70.
Diacu, F. & Holmes, P., Celestial Encounters. The Origins of Chaos and Stability. Princeton Univ. Press, Princeton, NJ, 1996.
Ginoux, J.-M. & Gerini, C., Henri Poincaré. A Biography Through the Daily Papers. World Scientific, Hackensack, NJ, 2014.
Gray, J., Henri Poincaré. A Scientific Biography. Princeton Univ. Press, Princeton, NJ, 2013.
Kautz, R., Chaos. The Science of Predictable Random Motion. Oxford Univ. Press, Oxford, 2011.
Lorenz, E. N., Deterministic nonperiodic flow. J. Atmos. Sci., 20 (1963), 130-141.
Mittag-Leffler, G., Zur Biographie von Weierstrass. Acta Math., 35 (1912), 29-65.
Peterson, I., Newtons Clock. Chaos in the Solar System. Freeman, New York, 1993.
Poincaré, H., Les méthodes nouvelles de la mécanique céleste, I-III. Gauthier-Villars, Paris, 1892-1899. (Also in English translation: New Methods of Celestial Mechanics, with an introduction by D. L. Goroff. American Institute of Physics, New York, 1993.)
Poincaré, H., Lettres à M. Mittag-Leffler concernant le mémoire couronné du prix de S. M. le roi Oscar II. Acta Math., 38 (1921), 161-173.
Stewart, I., Does God Play Dice? The New Mathematics of Chaos. Blackwell, Oxford, 1989.
Stubhaug, A., Gösta Mittag-Leffler. A Man of Conviction. Springer, Berlin-Heidelberg, 2010.
Sundman, K. F., Mémoire sur le problème des trois corps. Acta Mathematica, 36 (1912), 105-179.
Verhulst, F., Henri Poincaré. Impatient Genius. Springer, New York, 2012.
Wang, Q. D., The global solution of the n-body problem. Celestial Mech. Dynam. Astronom., 50 (1991), 73-88.